It sounds simple, I agree. But the problem is like designing a car. You could simply put some wheels together with simple set of chains and create a “car” that moves in your front lawn. But then if you want to design a professional car, you’ll spend much more time and professionalism to do it. And if you wanna build a sports car, you’ll have to fine tune every single parameter of your components to push the edge of what you can achieve.

This story doesn’t apply only to coils, but everything you design (actually I learned it from a book called “Professional C++” in a chapter discussing efficiency of algorithm writing, it’s not far from this case).

Concerning coils, if you just want to generate a few micro Tesla with no concerns about the homogeneity for the coil you’re designing, then it doesn’t matter how you do it. You could just wind a bunch of wires on your hand and your done. Today I’m not talking about such a thing. Today I’m gonna talk about coils that you want to use to generate relatively huge fields, with reasonable homogeneity.

For such specifications, if you’re careless about the details, you may end up wasting lots of time for experimental experience and money for cooling and power supplies. If you plan it carefully, you’ll save lots of money.

Parameters of the system

Any coils you design to generate magnetic fields will have a set of parameters that you have to tune. From those parameters I mention:

• Dimensions and geometry of the coils

• Magnetic field to be generated

• Thickness of the wires to be used

Where to start

The first thing one should determine for a coil system is the geometry of the coils. This is because the purpose of the coils is not just to generate a field, period. But it’s to generate a field over some region that is well defined for a specific experiment. One should know in advance what sample will be exposed to the magnetic field. If you don’t know that, you could spend days working on your coils, and eventually find out that your coils don’t fit your sample, or that your coils are so huge that you’re wasting so much power to generate fields you don’t need (math will show how important the size of your coils vs power is).

Therefore, start by defining the geometry of your coils. Once you know some characteristic radius or length of your coils, you have one step done. One more thing to pre-define, is how much wiring volume you want to use.

Optimum coil thickness

Any person starting with designing coils will have this question in mind: What’s the optimum wire thickness that should be used to have the optimum magnetic field. Guess what? If you know how much wire-volume you will use, then it doesn’t matter at all. Let’s do the math to verify this.

Suppose you have a slot to wind your wires that have a diameter $d$, and the slot has width $w$ and height $h$, as the figure shows. How can we optimally fill your wires in it? The optimal way is what the figure shows; it’s called “hexagonal packing”. This is in case we ignore third dimension’s problems, such as diagonal wires in the slots. This is a good approximation if the wires are wound carefully.

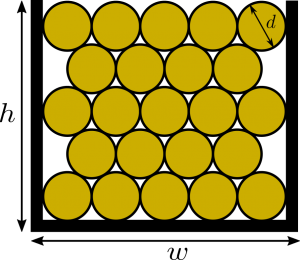
Notice that it’s very important to have a high number of circles per direction. This is to make sure that the flow of the current will be homogeneous in the volume. Imagine the opposite case, if you have one circle with diameter $d=h$. This will modify the magnetic field you expect from the wire as all the calculations of the magnetic field from a wire assume an infinitesimally thin wire.

With that said, let’s calculate the magnetic field from such a configuration. Any magnetic field generated from a current has the following form using the Biot-Savart law or Ampere’s law:

$$B=U\left(r\right)\cdot n\cdot I,$$

where $U\left(r\right)$ is a coefficient that depends on the dimensions of the coils with radius $r$, and $I$ is the electrical current, and $n$ is the number of total turns of the coil. We assumed that we know the geometry of your coil, meaning that $U\left(r\right)$ is fixed before starting this calculation. Let’s see how the wire diameter will modify your magnetic field.

From the definition of resistivity of a wire, we have

$$R=\rho\frac{\ell}{A}=\rho\frac{4\ell}{\pi d^{2}},$$

where R
is the resistance of the wire, $\ell$ is its length, $A=\pi\left(\frac{d} {2}\right)^{2}$ is its cross sectional area and $\rho$ is its resistivity. On the other hand, the power to be exerted on the coil is given by the formula

$$P=I^{2}R\quad\rightrightarrows \quad I=\sqrt{\frac{P}{R}},$$

and from the resistivity formula

$$I=\sqrt{\frac{P}{R}}=\frac{d}{2}\sqrt{\frac{\pi P}{\rho\ell}},$$

and we can put this in a form proportional to the magnetic field

$$B\propto n\cdot I=n\frac{d}{2}\sqrt{\frac{\pi P}{\rho\ell}}$$

There’s still one more question remaining to settle this; what’s the length of the wire required? The length of the wire depends on the diameter of the wire that will be used, since a thicker wire will occupy the area of the slot faster. Whether you wind your wire on a circle or a square, the length of the wire used will depend linearly on the side length or diameter of that geometry. If we call that $r$, then the length of the wire going to be $\ell=n\cdot k\cdot r$, where $k$ is $2\pi$ for a coil on the shape of a circle, and $4$ for a square coil, and $n$ is the number of turns. The formula of current then becomes:

$$n\cdot I=n\frac{d}{2}\sqrt{\frac{\pi P}{\rho\ell}}=n\frac{d}{2}\sqrt{\frac{\pi P}{\rho n\cdot k\cdot r}}=\frac{d}{2}\sqrt{\frac{\pi nP}{\rho\cdot k\cdot r}}.$$

Finally, the number of turns can be seen as the number of circles stacked in a hexagonal packing (as shown in the figure of the hexagonal packing). The number of circles (or cylindrical wires) with diameter $d$ packed in a slot of width $w$ and height $h$ can be approximated assuming a high number of circles (cylinders) per direction

$$n=\frac{w}{d}\cdot\frac{h}{d\cos30^{\circ}}=\frac{2}{\sqrt{3}}\frac{wh}{d^{2}},$$

where the factor $\cos30^{\circ}$ is simply due to the space saved with the hexagonal packing. In fact it doesn’t matter what packing you choose, since all packings will depend inversely on $d^{2}$, which is the important part. With this, the current formula becomes:

$$n\cdot I=\frac{d}{2}\sqrt{\frac{\pi nP}{\rho\cdot k\cdot r}}=\frac{1}{2}\sqrt{\frac{2\pi}{\sqrt{3}}}\sqrt{\frac{ whP}{\rho k r}}.$$

This result shows that the field doesn’t depend on the wire that we choose or the current we use. The magnetic field depends only on the power if the geometry of the coil is fixed.

One more important result here is that the power required is linearly proportional to $r$, which means that if your coils would have half the radius, half the power will be required. Thus it’s considerably important to make the coils as small as possible.

How to choose the wire diameter?

Having the magnetic field not depend on the wire thickness doesn’t mean we can choose it arbitrarily. In fact, the wire determines a very important characteristic, which is the voltage and amperage that we will need to generate. It doesn’t make sense to make a coil that will require 150 amperes and 0.1 volts, and that’s what the wire diameter determines for you. The thinner the wire is, the more resistance the coil will have, and thus more voltage will be required.

Thus, to fine-tune the production of your coil, decide the diameter of the wire after choosing the power supply that has the appropriate voltage and amperage.

Conclusion

It’s intuitive to think that the amount of current will tell how much field you’ll get, this is from simple, classical electromagnetism. However, in reality, it doesn’t really depend on the current. This is because the choice of the current depends on other parameters that are prioritized, such as the geometry of the coils. If the geometry of the coils is fixed, then it doesn’t matter how much current you put, but what matters is practically how much power one will put in.

This result is important for high field generators, since higher fields will entail higher power requirement, leading to heating problems. If your coils generate more heat that your system can dissipate, then it makes sense to think beforehand whether to whether the geometry should be made smaller or different, since smaller geometry means less power requirement.