Neil deGrasse Tyson, you gotta fix this!
I am very happy that Neil Tyson made the series “Cosmos”, where it is another way to communicate science to people, which is necessary in this era. I, personally, haven’t watched it, because I’m a physicist and the guy usually talks about things I learned academically. However, my wife watched it… and she told me once: “Neil Tyson said that electrons disappear from one orbit and appear in another”… and she continued talking, while I interrupted and asked… what?! How could a physicist say that? That destroys the simplest rule in relativity!
And yes, he did say that, which is crazy actually, and I’m pretty shocked that this kind of mistake would come out of such a famous scientist. Look for yourself:
Why is that wrong?
Simply, because there is no reason to believe that this is the case. Back then, when Bohr provided his semi-classical solution of the hydrogen atom, those transitions were not understood very well, and they would’ve lead to such conflicts. But, do we still deal with Bohr’s model? Definitely not! We now know Quantum Mechanics.
Before delving into Quantum Mechanics, let me pose this question: Is there any experimental evidence that electrons “teleport” from one orbit to the other as Neil Tyson said? The answer is: NO! And if there is, please let me know about them in the comments.
So, even if we would assume that Bohr made a successful model that explains the hydrogen energy levels in steady state, does that mean that it can be blindly extended to explain the dynamics of electronic transitions? Definitely not! That’s not scientific at all.
Why is this not scientific? Because in science, we create models of natural phenomena, and then test them and try to disprove them. Now what we see in the case of Bohr’s model, is that it successfully explained atomic energy levels to a good accuracy, but there is no part in Bohr’s model that talks about transitions. Therefore, inferring blindly that electrons are only in those levels is… crazy!
On the other hand, this easily breaks special relativity’s main result: Particles do not exceed the speed of light. So, what does this mean? This means that if what Neil Tyson said is true, then Quantum Field Theory, which is a superset of Quantum Mechanics, agrees that nothing exceeds the speed of light, but the very simple hydrogen atom in Quantum Mechanics… does not. How crazy is that?
Quantum Mechanics and the hydrogen atom
Explaining the Quantum Mechanics (QM) model, the QM model comes up when solving the Schrödinger equation (time independent version of it), and the result from solving that is a wave-function, where this wave-function is directly related to the probability of finding an electron spatially somewhere.
In the case of a hydrogen atom, the Schrödinger equation is solved for simply a negative electron and a positive proton. The result of this problem is presented in a wave-function that uses complicated mathematical functions, called Legendre Polynomials and Spherical Harmonics. The result is presented in a nice picture that I found on Wikipedia.
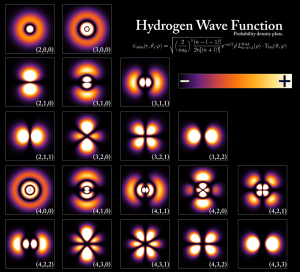 Notice that the solution is not “black and white” like Neil Tyson described it. There’s a key on the right, where a $+$ and $-$ can be seen. The $+$ represents higher probability than the $-$ regions. The first row shows the typical spherical orbits that we understand from classical mechanics (the Bohr model), while the other rows show more complicated solutions that involve angular momentum.
Notice that the solution is not “black and white” like Neil Tyson described it. There’s a key on the right, where a $+$ and $-$ can be seen. The $+$ represents higher probability than the $-$ regions. The first row shows the typical spherical orbits that we understand from classical mechanics (the Bohr model), while the other rows show more complicated solutions that involve angular momentum.
Notice that in those solutions, the wave-function is never zero anywhere but at infinity and specific points (lines, or nodes) in space that are infinitely small (Thanks to Lance for making me notice that more nodes exist in the wave-function)! So, according to our current knowledge of the hydrogen atom, why should we believe that electrons disappear from level to another? I think there’s no reason whatsoever.
A little more detail on transitions
Many atomic physics books treated the problem of atomic transitions in a model called “Dipole Transitions”. The model is usually accurate with relative accuracy of around $10^{-6}$. In that model, the problem of transitions is very well understood. For example, in the book Optically Polarized Atoms: Understanding light-atom interactions, there is a section called “Visualization of atomic transitions”. In it, the author shows that a transition from one state to another can be well modeled with a simple time evolution operator that incorporates the two involved states.
For a transition from state $\left|2P\right\rangle$ to the state $\left|1S\right\rangle$ can be modeled with a simple wave function
$$\psi=a_{1}\left|1S\right\rangle +e^{-i\frac{E_{2}-E_{1}}{\hbar}t}a_{2}\left|2P\right\rangle$$
where $a_1,a_2$ are normalization factors, and $E_1,E_2$ are the energies of the states. We see that an oscillation of frequency (in units of energy) $E_2-E_1$ would happen, leading to the production of a photon. Then, again, why should we ever believe that electrons teleport from one atomic state to the other?
Is it just simplicity?
Probably some people will argue that Neil Tyson was simplifying the atomic model for common people, but then I would ask the question: When did simplifications start to communicate false or wrong information? I think simplifying does not justify giving people wrong information at all.
Another simpler mistake
One more simple mistake Neil Tyson did in that video, is that he claimed that spontaneous decays are not understood (with why they happen). This is actually not true. In the same book I mentioned above, a discussion was put on that spontaneous decays happen due to spontaneous quantum fluctuations, that act as a stimulus for atoms and hit them. Therefore, technically, spontaneous decays do not exist; they’re just another form of stimulated emission.
This is not a big deal, though. I think this is an advanced issue, and claiming that “we don’t know” is better than posing wrong information.
Conclusion and discussion
I didn’t make this article to blame Neil Tyson, and actually he’s done a very good job with Cosmos. But I made this article because I found it common in social networks that people use this wrong information, and it has to be cleared out. I actually would be very grateful to him if he would fix this mistake and replace the episode.
The conclusion of this article, is that electrons do not teleport from one energy level to the other. There’s no evidence on that whatsoever! Electrons are, also, not strictly bound to those energy levels. According to our understanding of the quantum world, electrons have a probability cloud; and an electronic transition (dipole transition) will just make this cloud oscillate continuously from one energy level to another one continuously.

There are 2 things that seem to be in error. You stated “… the wave function is never zero anywhere but at infinity!” about atomic orbitals. Actually, that is only true for 1S, all the others have nodes where the function passes through zero. Second, you assumed that a hypothesis was a fact when you stated “… that spontaneous decays happen due to spontaneous quantum fluctuations …” There is no indications of spontaneous quantum fluctuations and whether they can cause spontaneous decays (although it is likely).
About the wave-function, you’re right. I will fix it. But about the spontaneous fluctuations, the book stated that this is something proven, the following is a quote from the book page 128:
———————-
Spontaneous vs. stimulated transitions
When an atom in the lower state absorbs radiation and is transferred to the upper state, it is clear that
the radiation is the agent which initiates the transition. But what if the atom is initially in the upper
state and there is no light shining on it. We know that, eventually, the atom will decay via spontaneous
emission. The question is: what causes the atom in a stationary state to spontaneously radiate an
electromagnetic wave and undergo a transition to the lower final state?
It turns out that the answer to this question is actually beyond nonrelativistic quantum mechanics,
and, to be answered properly, requires one to go into the realm of quantum electrodynamics, and,
more generally, the quantum field theory. The gist of the story is that, even in the absence of applied
light there is a certain density of electromagnetic-field fluctuations with all possible frequencies and
polarizations that exists in what would otherwise be considered the vacuum. This means that if a free
atom is in the upper state, there is always a vacuum fluctuation with a frequency and polarization
that is needed to connect resonantly the upper and the lower states of the atom, which causes a
spontaneous decay to occur. Thus, we can say that, in some sense, spontaneous emission is, in fact,
stimulated emission induced by vacuum fluctuations. A thorough introduction to quantum field theory
and quantum vacuum can be found in the book by Milonni (1994).
———————-
Is it a hypothesis? I don’t think so. I think it’s a successful model.
I HAVE No idea about more than half the stuff in this post, but you made it pretty clear i shuldnt have taken everything stated in cosmos as fact. The “electron jump” thing sounded so cool. :'(
however don’t go so strongly against tyson with your proofs. Understandings of these mechanics can change entirely, maybe to the extent of destroying understanding of relativity. Be a bit more open minded and more calm at the mistakes people make. Dont shout at your poor old wife.
I have just finished watching the Cosmos for the first time, and really enjoyed it, most of it was already known to myself but a great way to get the kiddies excited about science. Regarding the spontaneous decay of the hydrogen electron from one energy level to another which in theory is impossible ( or is it ) Perhaps and just perhaps, it is not the same electron hopping between orbits but a different electron from another hydrogen atom. A sort of social networking between the atoms passing information to each other via a dimension unknown to us on a quantum level. just a thought.
I am thinking of adding this to my list of Tyson bloopers: http://hopsblog-hop.blogspot.com/2016/01/fact-checking-neil-degrasse-tyson.html
But I don’t know much about quantum mechanics. I have been wanting to study quantum mechanics but have a limited supply of time and energy.
Oh, sure. No problem. I just hope you don’t attack “science” per se with some religious agenda. Otherwise, feel free to quote whatever you like from here.
Best,
Sam
Wow. I cant thank you enough for posting this. Last semester, in physics class we were taught that the electron teleported from one energy level to the next. I’m glad you cleared that up. You burst my wide-eyed, magic, wonder bubble, about teleportation as a possibility but I’m glad you did.
You’re a physicist? I’m assuming that somehow you’ve managed to avoid ever teaching, however. And you’ve never really thought about the philosophy of science at all.
Yeah, what Tyson said was an approximation. What you’ve said is a better approximation. But it’s still an approximation – remember, in QFT, particles like electrons are not what’s “really” going on. The fields behave like particles in certain circumstances. And QFT itself is an approximation, an effective field theory for what’s “really” happening.
A physicist knows that what’s important is to use an approximation that is good enough for what you’re calculating. A teacher knows that it’s also important to use an approximation your audience can understand.
And the wording you’ve quoted for Tyson is accurate even at the level of intro non-relativistic* quantum mechanics (upper-level undergrad or intro grad school). Electrons do “disappear” from, say, 1s, and appear in 2p. Notice we said nothing about distance there. The orbitals don’t correspond to distances, as you yourself pointed out. If you want a better interpretation of measurement than this (default Copenhagen), you need to look at more sophisticated formulations like Everettian QM.
*Let’s stress again that basic QM is non-relativistic. Your constraint from relativity literally doesn’t make sense within this theory. If you want to properly obey SR, you need QFT.
Mr. “Actual physicist”, apart from your hostile attitude, while parts of what you said are correct, and nothing in what I said is incorrect, which led you to wrestling with me on an opinion-based matter and you provided ZERO evidence or references (unlike me), you made a few mistakes yourself that show that you’re not that brilliant a physicist you think you are. I’m not here to judge you as you want to judge me, but take two steps back and think about why you’re doing this. You’re not proving me to be less in any way. You wanna know about approximations? Go ahead and take a look at my doctoral dissertation, and just search for the word “approximation”.
Anyone reading your comment will sense your hostility + not a single reference/evidence given to anything you said! And a reader will just wonder why you’re doing this. So why are you doing this? Do you just want to prove you’re a “better” physicist than me? OK, dude, you get a star! Congrats!
Here are your mistakes:
1- Orbitals ARE really distances. Where the hell did I say they’re not real distances? When we solve the Schrödinger’s equation, we use a RADIUS in the potential, and we derive the RADIUS of the hydrogen atom, $a_0$, which is called the Bohr RADIUS. What does judge whether it’s a real radius? It’s basically the RADIUS that you see in your equations. It’s not your opinion. It’s not an opinion-based matter. Here is a link where you can learn about atomic orbitals and how they’re related to RADIUS.
https://en.wikipedia.org/wiki/Atomic_orbital
2- Transitions from 1s to 2p do involve a change in radius (from orbital n=1 to orbital n=2), and does involve a change in angular momentum. Ever seen the hydrogen wave-functions?
3- Even if orbitals are not real in a physical radius matter (which they are, but let’s just say they aren’t), that doesn’t necessarily mean that transitions over atomic states have to be instantaneous unless you prove that; i.e., disappear at one state and appear in the other state. While constraints on physical radius transitions are bound to relativity, since change in distance over time is speed, other instantaneous transitions will have their problems too. It’s more reasonable to consider a superposition between the initial and final states, where the wave function dacays from one and grows for the other using an Evolution Operator, which I used to describe atomic transitions in my article (ever heard about it? Ever learned how wave-functions and operators evolve over time?). At least that’s a superset of what you said! Why would any physicist in the world accept your crude, unrealistic model and take it for given as a general solution to every possible atomic system? Just because they can’t disprove it (which is still not true)? How about you believe in unicorns because you can’t disprove them too?
Look, I’m more than happy to discuss things with you in detail like civilized people, but I’m not really willing to have a battle with hostile behavior. Your next comment will only be accepted if you stop your hostility.
Actually, to be clear, I was being condescending, not hostile. You are now being hostile. I’ll try to not be condescending anymore, but I am going to correct you where you’re wrong.
Looking at your publications, you are a legit physicist. Good for you. This makes me a lot more puzzled about why you don’t appear to know basic QM.
1. Orbitals are not distances. They really aren’t. Orbitals are defined by the n,l,m quantum numbers (reference: any basic quantum book; e.g., Shankar, Griffiths, etc.). The expectation value of the r operator does depend on this (well, kinda – it depends on n and l, not m, so is the same for all electrons within a subshell). But r, as you very well know, is an operator, not a number that’s defined for a given |nlm>. (This is why we use quantum numbers like n, l, and m – because position and momentum, which define our particle state in classical phase space, are generally no longer well-defined things in Hilbert space. Source: any basic QM book. Seriously.)
2. No, they don’t. They involve a change in the expectation value of the radius. Why do you keep conflating operators with quantities? They do change the angular momentum, which is well defined because |nlm> is an eigenstate of L^2. It’s not an eigenstate of the operator r.
3. You seriously appear to be using a Bohr model of the atom. Of course this will make you worried about “instantaneously” transitioning states. Sure, the wavefunction evolves smoothly, according to Schrödinger. (Unless you measure it, in your Copenhagen interpretation, then it doesn’t! Hence my recommendation for Everettian QM.)
4. Can you address the fact that non-relativistic QM is non-relativistic? Don’t get all worked up about things the model can’t accommodate. You are getting incredibly worked up over a really minor simplification that Tyson made.
1 and 2- Orbitals are defined by $n,l,m$, right. Did I say that’s not true? I never have. But what I said was that these numbers ARE RELATED TO RADIUS. If you look at the Schrödinger equation solution of the Hydrogen atom, you’ll see that the wave function is a function $\psi_{nlm} (r,\theta,\phi)$. What is $r$? Isn’t that a radius? Doesn’t a specific $n$ have a higher likelihood for a specific radius? You call it an operator? Some quantum mechanics books call it an OBSERVABLE. It’s something that is MEASURABLE. It’s the closest thing to a real measurable quantity in Quantum Mechanics. What’s the part that doesn’t make it real for you? I honestly have no idea.
3- No, it’s not just the Bohr model I’m using. It’s also quantum mechanics which is a superset of the Bohr’s model. There are tons of reasons why not to accept instantaneous transitions, and while I mentioned one here and more than one in the article, I still have more. All that’s Tyson doing there is a very crude zeroth order interpolation. Sorry! Science doesn’t work that way, as far as I know. At least don’t tell people that this is the way it works. You can always avoid talking about such confusing things, hence this article.
4- Yes, I agree with you completely. Non-relativistic QM is non-relativistic. But again, even if we ignore relativity, it doesn’t justify accepting the crude zeroth order interpolation Tyson did.
You may find it a little slip as an approximation. I find it a big deal because people started asking me after this, and then it’s a problem for me to justify this very non-realistic and odd behavior Tyson gave as a fact to people. All I’m saying is that there are things we know with very high certainty that you can teach to the public, while this whole “instantaneous” jump between levels isn’t any close to anything true, especially that the public doesn’t understand that physics is just modeling nature, and not the absolute truth about nature.
Peace!
I just noticed in the original post, when you show the spherical harmonics plot: “The first row shows the typical spherical orbits that we understand from classical mechanics, while the other rows show more complicated solutions that involve angular momentum.”
I’m puzzled by this statement. Yes, the l=0 states are spherically symmetric, but this is not a classical thing. The radial portion comes from solving the Schrödinger equation, just like the rest of it. It’s related to probability density, and has no classical analog. (In classical mechanics, the 1/r potential can have any you want, for example. Hence the “quantum” in quantum mechanics.) Classical orbits of course don’t have to be spherical, either. (As in the QM case, that’s just the lowest angular momentum state for a given energy.)
I’d suggest you correct it, but you went a bit wild last time I made such a suggestion. Just a tip for continuing in your field (I hadn’t realized how young you were until I looked at your dissertation): you need to substantively address criticism with good arguments if the criticism is wrong, and corrections if the criticism is right. You did that on a couple minor issues above, but on mine… And yes, citations are good, but don’t expect people to cite things found in standard intro-level texts in courses we all had to take to get PhDs.
The classical thing I’m talking about is the Bohr model. The Bohr model was able to predict the principal energy levels quite accurately, which are spherically symmetric, by definition, as they’re defined to have constant radius. Check the Bohr model to remember this. The condition of atom stability in Bohr’s model is $n\lambda=2\pi r$. If you think of classical orbits as earth’s orbit around the sun, then you went too far, as I never said that; not even close. A reasonable improvement to the article is only putting in parenthesis that it’s the (Bohr model). Nothing I said there is wrong, is it?
I’m happy to address criticism and I did it before. But when you become hostile or condescending + unclear + opinion driven, then you make it hard for me. We all do mistakes, which is something I understand very well, but here you took your misunderstanding as my mistakes with a bad attitude.
It has to teleport, if they didnt teleport, then the black spaces in between the orange wouldiunt be black, DUH. And if it only traveled rarely, then only one side of the atom would be bright orange, but both sides are bright, check mate!